 電気工事士技能試験セット KP-001 |
 NEW DROP ウォータプライヤー (BWP-250) |
 マーベル MARVEL VA線ケーブルストリッパー JVA-123 [A011215] |
 VESSEL(ベッセル)VAストリッパー 3200VA-1 |
 ロブスター(エビ印)ロブテックス LOBSTER エコ電線対応 VVF線ストリッパー EEF203 |
 次回使える送料無料クーポンついてます電気工事士技能試験必携!【送料無料】VESSEL VA線スト... |
 第二種電気工事士技能試験器具・消耗品セット 平成28年版 |
 第二種電気工事士技能試験ケーブルセット+器具・消耗品セット 平成28年版 |
 【在庫特価】ロブテックス(エビ印) 圧着工具リングスリーブ(E)用 AK17A |
 【即日発送】】【NEW】【電気工事士 技能試験練セット】【器具セット】★ボンド線止めネジま... |
![HOZAN(ホーザン)[S-19]電気工事士技能試験セット【2013ショップ・オブ・ザ・イヤー受賞店】...](http://hbb.afl.rakuten.co.jp/hgb/?pc=http%3a%2f%2fthumbnail.image.rakuten.co.jp%2f%400_mall%2fedenki%2fcabinet%2flobster01%2fed693861.jpg%3f_ex%3d128x128&m=http%3a%2f%2fthumbnail.image.rakuten.co.jp%2f%400_mall%2fedenki%2fcabinet%2flobster01%2fed693861.jpg%3f_ex%3d80x80) HOZAN(ホーザン)[S-19]電気工事士技能試験セット【2013ショップ・オブ・ザ・イヤー受賞店】... |
8.電圧降下
出題はほぼ毎年です。
見た目に難しそうな図が出てくるので、敬遠されがちですが難しくはないので、チャレンジしてください。
 電線にも僅かながらも抵抗があり、電圧を低下させます。
電線にも僅かながらも抵抗があり、電圧を低下させます。
一般住宅の屋内配線ぐらいではあまり気にする必要はありませんが、商業施設やビルなどになると無視できない問題です。
問題では、細かい部分にはこだわらないので、電線の抵抗と言っても、普通に抵抗と認識して計算するので安心してください。
電圧降下の計算問題で、使用するのはオームの法則とP(W)=IVです。
それ以外は使わずに問題を計算してゆきます。

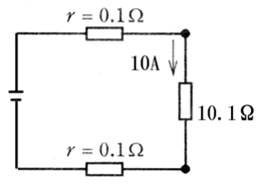
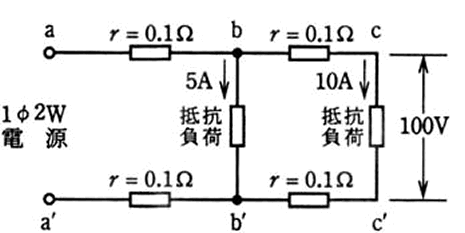
図のような単相2線式回路で、c-c’間の電圧が100〔V〕のとき、a-a’間の電圧〔V〕は。
ただし、r
は電線の電気抵抗〔Ω〕とする。
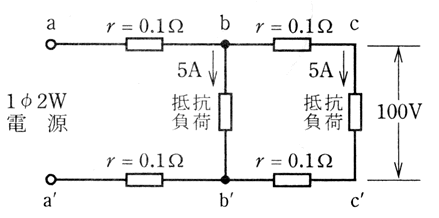
イ.102 ロ.103 ハ.104 ニ.105
まずは、問題文が何を言っているかを正しく理解しましょう。
 考え方としては「面倒だけど抵抗がたくさんついている」で問題ありません。
考え方としては「面倒だけど抵抗がたくさんついている」で問題ありません。
直列で接続されている抵抗(電線)で使われている電圧を、右側の100Vに加算すれば解答できます。
では、計算してゆきましょう。
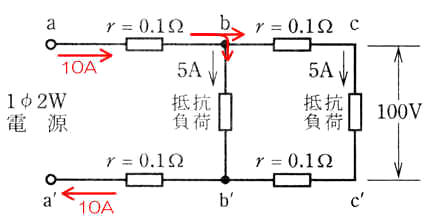
さて、抵抗負荷がある電線にそれぞれ5Aずつ流れているようです。
抵抗負荷は並列接続の関係ですから、分流しています。と、いうことは、元は10Aと言うことになります(図の通り)しかも電流は全体で一定ですから、反対側でも10Aです(図の通り)
これで計算の下準備は完了です。
a-b間の電圧を計算しましょう。
V=IR=10×0.1=1V
a’-b’間の電圧も条件が一緒なので1V
b-c間の電圧計算をしましょう。
V=IR=5×0.1=0.5V
b’-c’間の電圧も条件が一緒なので0.5V
電線の抵抗負荷で使われる電圧の合計は3Vです。 これを100Vと合計すれば103Vとなります。
抵抗負荷は並列接続で、分圧は起こっていません。ゆえに、無視できます。
なんだかよく分からない方のために、もっと計算して確認してみましょう。
回路を書き換えてみました。
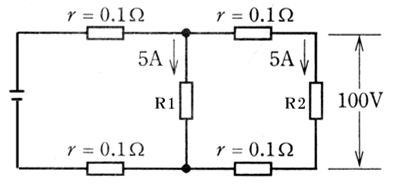 R2の抵抗を求めてみます。
R2の抵抗を求めてみます。
抵抗の両端が100V、流れる電流が5A
R=V/I=100/5=20Ω
右側の抵抗値の合計は0.1+20+0.1=20.2Ω
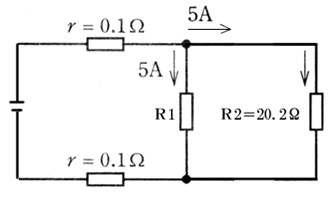 まとめるとこんな感じになりますが、合成抵抗なので、電圧を計算し直します。
まとめるとこんな感じになりますが、合成抵抗なので、電圧を計算し直します。
V=IR=5×20.2=101V
R1の抵抗を求めてみます。
並列接続では分岐しても電圧は分かれないので、R1にも101Vの電圧が掛かります。
R=V/I=101/5=20.2Ω R1とR2の合成抵抗は和分の積を使って計算すると、
(20.2×20.2)/(20.2+20.2)=408.04/40.4=10.1Ω
合成抵抗は0.1+10.1+0.1=10.3Ω
 これで電圧を求めると、
V=IR=10×10.3=103Vとなります。
これで電圧を求めると、
V=IR=10×10.3=103Vとなります。
![]()
これ以上複雑な回路は出題されませんので、直列部分の電圧を計算して、提示されている電圧と合計すれば答えが出ます。簡単に計算できるのですから、うろ覚えの式なんか使わないようにしてくださいね。

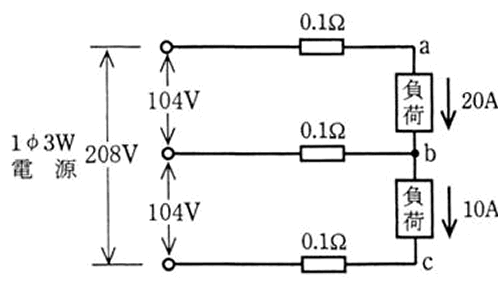
図のような単相3線式回路において、電線1線あたりの電気抵抗が0.1〔Ω〕のとき、ab間の電圧〔V〕は。
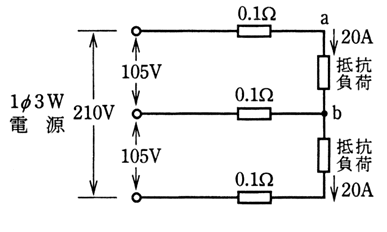
イ.97 ロ.100 ハ.103 ニ.106
単相3線式で抵抗負荷の値が同じであるとき〔負荷が平衡している〕といい、中性線と呼ばれる中の電線には、電気がうち消し合っているので電流は流れません。
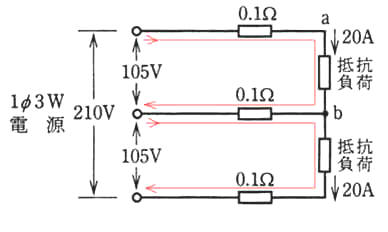 もしも、抵抗負荷が20Aと10Aの様に
もしも、抵抗負荷が20Aと10Aの様に
不平衡であると、中性線には差分の電流が流れます。差分の電流で計算した電線抵抗にかかる電圧が、大きな電流が流れている方にとっては電圧降下、小さな電流が流れている方にとっては電圧上昇となります。
話しを元に戻します。では、aの地点までの電線の抵抗だけを考えればよいので、電線に電圧がいくらかかっているかを計算しましょう。
V=IR=20×0.1=2V
したがって、a-b間の電圧は105V-2V=103Vと言うことになります。
正解は“ハ”です。
![]()
単相3線式は、中性線の扱いが重要です。

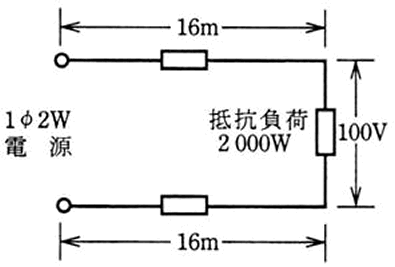
図のように、電線のこう長8〔m〕の配線により、消費電力2 000
〔W〕の抵抗負荷に電力を供給した結果、負荷の両端の電圧は100〔V〕であった。配線における電圧降下〔V〕は。
ただし、電線の電気抵抗は長さ1000〔m〕当たり3.2〔Ω〕とする。
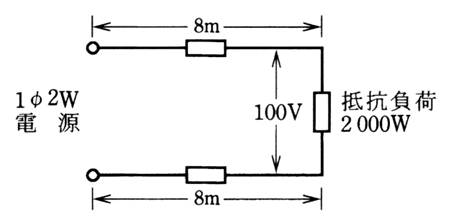
イ.1 ロ.2 ハ.3 ニ.4
この問題を解くのは、オームの法則だけでは解けません。
W(ワット)という単位が出てきています。
聞き慣れたこのワットという単位は、1時間あたりの電力です。
電力使用量ではkW・hという単位を使用します。キロに注意!1000倍です。
1000W(ワット)=1kW・h(キロワットアワー)
ワットはPと表され、どのように計算るかというと、P=VIです。
V=IRと間違わないようにしてくださいね。早速計算してみましょう。
オームの法則で電線にかかる電圧を算出したいのですが、電流Aの値が分かりません。電圧が分かっているのは2000Wの抵抗にかかる100Vだけです。
そこで、P=VIの登場です。
P=VIにとりあえず数字を当てはめてみます。
2000=100×I
つまり、I=2000/100です。
=20A これが電流です。
あとはオームの法則!と思いきや、もう一つ問題があります。電線の電気抵抗は長さ1000〔m〕当たり3.2〔Ω〕と提示されていますので、8m分の抵抗を算出します。
3.2×(8/1000)=0.0256Ω でもいいですし、
1000:3.2=8:X
1000X=25.6
X=0.0256Ω でもいいです。
好きな計算の仕方で8mあたりの抵抗を出してください。
ようやくオームの法則が使えます。
V=IR=20×0.0256=0.512
これが2本あるので、0.512×2=1.024V 約1V
正解は“イ”です。
![]()
P〔W〕=V〔V〕・I〔A〕の関係式を忘れないようにしましょう。
![]()
1.図のような単相2線式回路において、c-c’間の電圧が100〔V〕のとき、a-a’間の電圧〔V〕は。
ただし、rは電線の電気抵抗〔Ω〕とする。
イ.102 ロ.103 ハ.104 ニ.105
2.図のように、電線のこう長16〔m〕の配線により、消費電力2 000
〔W〕の抵抗負荷に電力を供給した結果、負荷の両端の電圧は100〔V〕であった。配線における電圧降下〔V〕は。
ただし、電線の電気抵抗は長さ1000〔m〕当たり3.2〔Ω〕とする。
イ.1 ロ.2 ハ.3 ニ.4
3.図のような単相3線式の回路において、ab間の電圧〔V〕、bc間の電圧〔V〕の組合せとして、正しいものは。
ただし、負荷は抵抗負荷とする。
イ.ab間:101 ロ.ab間:103 ハ.ab聞:102 二.ab間:101
bc間:100 bc聞:104 bc間:103 bc間:104
4.図のような単相2線式電路で、C-C'間の電圧は100〔V〕であった。A-A'が間の電圧〔V〕は
ただし、rは電線1線当たりの抵抗し、負荷の力率は100〔%〕とする。
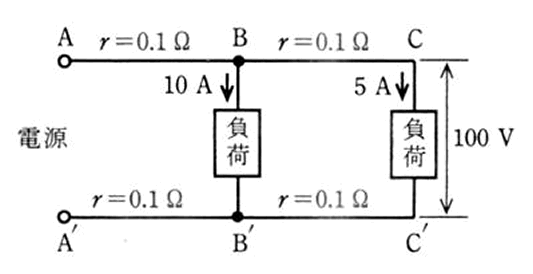
イ.102 ロ.103 ハ.104 ニ.105
![]()
1. ニ
a-b間の電圧を求めます。電流は10+5=15A
V=IR=15×0.1=1.5V a’-b’間も同じ1.5V
b-c間の電圧を求める。電流は10A
V=IR=10×0.1=1V b’-c’間も同じ1V
全ての電線の抵抗を合計すると1.5+1.5+1+1=5V
したがって、a-a’間の電圧は105V
2. ロ
回路の電流を求めます。
P=VIを変形しI=P/V=2000/100=20A
16m分の電線の抵抗は3.2×(16/1000)=0.0512
V=IR=0.0512×20=1.024V
これが2本あるので、1.024×2=2.048V 約2V
3. ニ
上の電線抵抗にかかる電圧を求めます。
V=IR=20×0.1=2V
負荷が不均衡なので、中の線には電流が流れます。
bから20A、電源から10Aなので、20A-10A=10Aの電流がbから電源方向に流れます。
中の電線抵抗にかかる電圧を求めます。
V=IR=10×0.1=1V a-b間は104-2-1=101V
b-c間に対しては中の電線抵抗は電圧上昇として働くため、(加算する)
104+1-1=104V
4. ハ
A-B間の電圧を求めます。電流は10+5=15A
V=IR=15×0.1=1.5V A’-B’間も同じ1.5V
B-C間の電圧を求めます。電流は5A
V=IR=5×0.1=0.5V B’-C’間も同じ0.5V
全ての電線の抵抗を合計すると1.5+1.5+0.5+0.5=4V
したがって、A-A’間の電圧は104V